Total idem
Blog mondain
Ca y est, voilà la période où je ne trouve plus trop le temps et l'inspiration pour le blog.
Cette (dernière) rentrée universitaire s'annonce pleine de défis. Au programme cette année, beaucoup plus d'autonomie dans le travail. En résumé, ça implique des heures de lecture, des heures de solitude, des heures à boire du thé sur un traversin pour amortir la rigidité de la chaise...
Puis il y a cette motivation croissante à se trouver du boulot, elle même accompagnée par l'envie de concrétiser quelques projets qui me tiennent à coeur.
Sans inspiration, le blog a tendance à être fade, égocentrique, craint la décadence de l'insignifiance... Les posts avenirs ressembleraient à ce que je je suis en train d'écrire maintenant. Trêve.
La programmation par contraintes
Dans le post concernant la résolution de Sudoku par un algorithme, j'ai mentionné une approche par la programmation par contraintes.
C'est en fouinant dans le télé journal que je suis tombé sur un jeu suranné aussi vicieux que le Sudoku, mais tout à fait approprié pour une résolution par contraintes.
Les règles du total idem
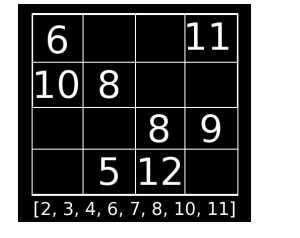
Etant donné cette grille et l'ensemble de valeurs [2, 3, 4, 6, 7, 8, 10, 11], il faut trouver une disposition de ces nombres dans les cases vides afin qu'une somme de trente soit obtenue sur chaque ligne et aussi sur chaque colonne. On a aussi pour contrainte que chaque nombre pris de l'ensemble de valeurs ne peut être utilisé qu'une fois.
Résoudre ce problème en utilisant une approche algorithmique purement impérative nécessite un peu d'ingéniosité, car à priori, il n'y aurait pas d'astuce évidente permettant d'élaguer le nombre des combinaisons possibles avant de trouver la solution. C'est justement à ce niveau que la programmation par contraintes peut nous être utile. Utile dans le sens où elle permet de s'abstraire du raisonnement opérationnel pour se concentrer sur la définition même du problème et par là, faciliter sa résolution.
L'idée, c'est de coder le problème en utilisant une liste comme structure de données et d'exprimer des contraintes sur cette liste. Prolog est un langage qui est utile pour la résolution de ce problème car il intègre à la fois les listes, un moteur d'inférence et des prédicats exprimant des contraintes.
PROgramming Language Of Gods
Merde, j'ai perdu un temps fou avec ce langage rien que pour manipuler les listes. Bref je poste le code et la solution de la grille. Pas de commentaire sur code. Il y a toujours la voie des commentaires pour celui ou celle qui voudrait plus d'infos.
Oups, j'allais oublié, j'ai utilisé SWI-Prolog.
Code Prolog
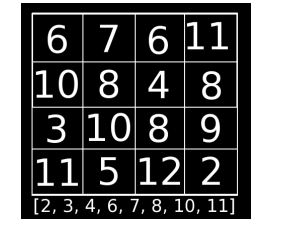
La solution
Ca y est, voilà la période où je ne trouve plus trop le temps et l'inspiration pour le blog.
Cette (dernière) rentrée universitaire s'annonce pleine de défis. Au programme cette année, beaucoup plus d'autonomie dans le travail. En résumé, ça implique des heures de lecture, des heures de solitude, des heures à boire du thé sur un traversin pour amortir la rigidité de la chaise...
Puis il y a cette motivation croissante à se trouver du boulot, elle même accompagnée par l'envie de concrétiser quelques projets qui me tiennent à coeur.
Sans inspiration, le blog a tendance à être fade, égocentrique, craint la décadence de l'insignifiance... Les posts avenirs ressembleraient à ce que je je suis en train d'écrire maintenant. Trêve.
La programmation par contraintes
Dans le post concernant la résolution de Sudoku par un algorithme, j'ai mentionné une approche par la programmation par contraintes.
C'est en fouinant dans le télé journal que je suis tombé sur un jeu suranné aussi vicieux que le Sudoku, mais tout à fait approprié pour une résolution par contraintes.
Les règles du total idem

Etant donné cette grille et l'ensemble de valeurs [2, 3, 4, 6, 7, 8, 10, 11], il faut trouver une disposition de ces nombres dans les cases vides afin qu'une somme de trente soit obtenue sur chaque ligne et aussi sur chaque colonne. On a aussi pour contrainte que chaque nombre pris de l'ensemble de valeurs ne peut être utilisé qu'une fois.
Résoudre ce problème en utilisant une approche algorithmique purement impérative nécessite un peu d'ingéniosité, car à priori, il n'y aurait pas d'astuce évidente permettant d'élaguer le nombre des combinaisons possibles avant de trouver la solution. C'est justement à ce niveau que la programmation par contraintes peut nous être utile. Utile dans le sens où elle permet de s'abstraire du raisonnement opérationnel pour se concentrer sur la définition même du problème et par là, faciliter sa résolution.
L'idée, c'est de coder le problème en utilisant une liste comme structure de données et d'exprimer des contraintes sur cette liste. Prolog est un langage qui est utile pour la résolution de ce problème car il intègre à la fois les listes, un moteur d'inférence et des prédicats exprimant des contraintes.
PROgramming Language Of Gods
Oups, j'allais oublié, j'ai utilisé SWI-Prolog.
Code Prolog
:- use_module(library('clp/bounds')).
:- use_module(library('clp/clp_distinct')).
% col(+Liste, +Nieme, -Col)
% Col est la Nieme colonne de la liste Liste
col([], _, []).
col([C1 | L], N, [E | C2]) :-
nth1(N, C1, E),
col(L, N, C2).
reverse(G, N, []) :-
length(G, N).
reverse(G, N, [C | R]) :-
N1 is N + 1,
col(G, N1, C),
reverse(G, N1, R).
%find_unification([E | L], V) :-
% var(E), % free variable
% dom(E, V).
% trouver une valeur pour E de L dans V
contraintes_aux([], _).
contraintes_aux([E | L], V) :-
nonvar(E), % var liée
contraintes_aux(L, V).
contraintes_aux([E | L], V) :-
var(E), % var libre
E in 0..30,
vars_in([E], V), % contrainte de domaine
select(E, V, V1), % extraire E de V
contraintes_aux(L, V1).
get_free([], []).
get_free([E | L], L1) :-
nonvar(E),
get_free(L, L1).
get_free([E | L], [E | L1]) :-
var(E),
get_free(L, L1).
% contraintes_lignes(+G, +V) ssi
% a une somme de 30
contraintes([], _).
contraintes([L | R], V) :-
get_free(L, L1),
contraintes_aux(L, V),
sum(L, #=, 30), % contrainte sur la somme
subtract(V, L1, V1),
contraintes(R, V1).
solve(G, V) :-
contraintes(G, V),
reverse(G, 0, T),
contraintes(T, V).
La solution



1 Comments:
Le code Prolog contient un bug dû à l'utilisation de subtract dans la relation contraintes/2
Le prédicat subtract s'applique sur un ensemble et pas une liste.
Donc si on a une liste L=[1,2,2,3], subtract(L, [2], R) donne R=[1,3]
Je laisse le soin au lecteur de trouver (et de partager) la solution au problème.
Enregistrer un commentaire
<< Home