La preuve de la semaine
Bienvenue à toi à ce rendez-vous semestriel.
Tout d'abord merci au commentaire anonyme sur le dernier post qui fait ressortir une erreur dans la preuve. Ma réponse précise l'erreur d'écriture faite et apporte une correction.
Cette semaine je parlerai sommairement des nombres premiers pour ensuite m'intéresser à la preuve démontrant leur infinité.
Qu'est-ce qu'un nombre premier
Un nombre n est un premier si et seulement si:
L'intérêt du nombre premier.
En informatique on s'intéresse aux nombres premiers dans le domaine de la cryptologie (voir l'algorithme RSA). En effet le test de primalité - qui consiste à décider si un nombre est premier ou non - bien qu'ayant des algorithmes polynomiaux, reste dans la pratique un problème difficile.
Proposition intermédiaire
Pour cette preuve nous nous appuierons sur le théorème fondamental de l'arithmétique qui dit que tout nombre composé supérieur à 1 peut être écrit sous la forme d'un produit de facteurs premiers.
La preuve d'Euclide
Il existe une infinité de nombres premiers.
Pour s'en convaincre nous procédons par un raisonnement par l'absurde.
Faisons l'hypothèse que , l'ensemble des nombres premiers, soit fini. Nous pouvons alors énumérer de façon exhaustive ses éléments:
, l'ensemble des nombres premiers, soit fini. Nous pouvons alors énumérer de façon exhaustive ses éléments:

Nous posons . Alors deux cas se présentent:
. Alors deux cas se présentent:
1.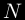 est premier.
est premier.
Si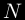 est premier, alors
est premier, alors  . Donc nous avons bien une contraction de l'hypothèse.
. Donc nous avons bien une contraction de l'hypothèse.
2.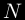 est un nombre composé.
est un nombre composé.
Si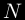 est composé, alors on peut l'écrire comme un produit de facteurs premiers. Or
est composé, alors on peut l'écrire comme un produit de facteurs premiers. Or  ,
, 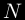 divisé par
divisé par  aurait pour reste 1. D'où l'existence de facteurs premiers n'étant pas inclut dans
aurait pour reste 1. D'où l'existence de facteurs premiers n'étant pas inclut dans  . Ce qui contredit l'hypothèse.
. Ce qui contredit l'hypothèse.
Nous pouvons alors conclure qu'il existe bien une infinité de nombres premiers.
Tout d'abord merci au commentaire anonyme sur le dernier post qui fait ressortir une erreur dans la preuve. Ma réponse précise l'erreur d'écriture faite et apporte une correction.
Cette semaine je parlerai sommairement des nombres premiers pour ensuite m'intéresser à la preuve démontrant leur infinité.
Qu'est-ce qu'un nombre premier
Un nombre n est un premier si et seulement si:
- n > 1
- n n'a que deux diviseurs, 1 et n
L'intérêt du nombre premier.
En informatique on s'intéresse aux nombres premiers dans le domaine de la cryptologie (voir l'algorithme RSA). En effet le test de primalité - qui consiste à décider si un nombre est premier ou non - bien qu'ayant des algorithmes polynomiaux, reste dans la pratique un problème difficile.
Proposition intermédiaire
Pour cette preuve nous nous appuierons sur le théorème fondamental de l'arithmétique qui dit que tout nombre composé supérieur à 1 peut être écrit sous la forme d'un produit de facteurs premiers.
La preuve d'Euclide
Il existe une infinité de nombres premiers.
Pour s'en convaincre nous procédons par un raisonnement par l'absurde.
Faisons l'hypothèse que
 , l'ensemble des nombres premiers, soit fini. Nous pouvons alors énumérer de façon exhaustive ses éléments:
, l'ensemble des nombres premiers, soit fini. Nous pouvons alors énumérer de façon exhaustive ses éléments:
Nous posons
 . Alors deux cas se présentent:
. Alors deux cas se présentent:1.
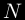 est premier.
est premier.Si
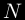 est premier, alors
est premier, alors  . Donc nous avons bien une contraction de l'hypothèse.
. Donc nous avons bien une contraction de l'hypothèse.2.
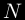 est un nombre composé.
est un nombre composé.Si
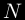 est composé, alors on peut l'écrire comme un produit de facteurs premiers. Or
est composé, alors on peut l'écrire comme un produit de facteurs premiers. Or  ,
, 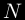 divisé par
divisé par  aurait pour reste 1. D'où l'existence de facteurs premiers n'étant pas inclut dans
aurait pour reste 1. D'où l'existence de facteurs premiers n'étant pas inclut dans  . Ce qui contredit l'hypothèse.
. Ce qui contredit l'hypothèse.Nous pouvons alors conclure qu'il existe bien une infinité de nombres premiers.


0 Comments:
Enregistrer un commentaire
<< Home