La preuve de la semaine
Cher lecteur,
me revoilà cette semaine avec encore une preuve triviale issue de la théorie des nombres. Nous cherchons à démontrer qu'il existe deux nombres irrationnels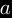 et
et  tels que
tels que 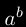 soit rationnel.
soit rationnel.
Qu'est-ce qu'un nombre rationnel?
Un nombre rationnel est un nombre qui peut s'écrire sous la forme d'une fraction, notamment
qui peut s'écrire sous la forme d'une fraction, notamment 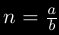 . La forme duale étant le nombre irrationnel.
. La forme duale étant le nombre irrationnel.
Première étape
Pour les besoins de la preuve nous établirons en premier lieu
l'irrationalité de . Pour cela nous procédons par un raisonnement par l'absurde.
. Pour cela nous procédons par un raisonnement par l'absurde.
Faisons l'hypothèse que soit rationnel. Alors
soit rationnel. Alors  , tels que
, tels que  , pour
, pour 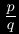 une fraction irréductible (pour
une fraction irréductible (pour  non nul).
non nul).
Nous élevons l'équation posée au carré pour obtenir
Donc nous avons qui nous permet de dire que
qui nous permet de dire que 
est divisible par deux. Comme est un nombre pair,
est un nombre pair,  l'est aussi.
l'est aussi.
Or si est divisible par deux, alors
est divisible par deux, alors  tel que
tel que  .
.
Nous pouvons alors écrire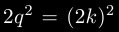 et donc
et donc  . Maintenant nous constatons que
. Maintenant nous constatons que  est divisible par deux, donc a fortiori
est divisible par deux, donc a fortiori  aussi.
aussi.
Nous avons obtenu et
et  divisible par deux, or nous avons supposé
divisible par deux, or nous avons supposé  et
et  premiers entre eux, donc il y a bien contraction de l'hypothèse.
premiers entre eux, donc il y a bien contraction de l'hypothèse.
Alors est un nombre irrationnel. (CQFD)
est un nombre irrationnel. (CQFD)
Et maintenant la preuve.
Démontrons maintenant qu'il existe deux nombres irrationnels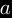 et
et  tels que
tels que 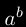 soit rationnel.
soit rationnel.
Notre preuve s'appuie sur la loi du tiers exclu qui en formulation
simple suppose qu'une proposition est soit vraie ou fausse.
Posons et
et  .
.
Nous avons et deux cas se présentent:
et deux cas se présentent:
1) Soit est un nombre rationnel, dans quel cas nous avons trouvé un rationnel validant la proposition.
est un nombre rationnel, dans quel cas nous avons trouvé un rationnel validant la proposition.
2) Soit est irrationnel.
est irrationnel.
Dans quel cas nous posons et
et  . En effet, nous avons bien établi l'irrationalité de
. En effet, nous avons bien établi l'irrationalité de  et nous avons
et nous avons  .
.
En simplifiant, nous obtenons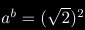 , soit
, soit  , un rationnel.
, un rationnel.
Dans les deux cas, nous obtenons un nombre rationnel.
Mot de la fin
Cette preuve est d'autant plus intéressante qu'elle fait appel au principe du tiers exclu qui est un raisonnement logique rejetté dans une démonstration constructive.
!Erreur!
Je remercie le commentaire anonyme pour avoir signalé l'erreur dans cette preuve. Voir les commentaires.
me revoilà cette semaine avec encore une preuve triviale issue de la théorie des nombres. Nous cherchons à démontrer qu'il existe deux nombres irrationnels
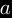 et
et  tels que
tels que 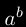 soit rationnel.
soit rationnel.Qu'est-ce qu'un nombre rationnel?
Un nombre rationnel est un nombre
 qui peut s'écrire sous la forme d'une fraction, notamment
qui peut s'écrire sous la forme d'une fraction, notamment 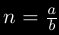 . La forme duale étant le nombre irrationnel.
. La forme duale étant le nombre irrationnel.Première étape
Pour les besoins de la preuve nous établirons en premier lieu
l'irrationalité de
 . Pour cela nous procédons par un raisonnement par l'absurde.
. Pour cela nous procédons par un raisonnement par l'absurde.Faisons l'hypothèse que
 soit rationnel. Alors
soit rationnel. Alors  , tels que
, tels que  , pour
, pour 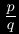 une fraction irréductible (pour
une fraction irréductible (pour  non nul).
non nul).Nous élevons l'équation posée au carré pour obtenir

Donc nous avons
 qui nous permet de dire que
qui nous permet de dire que 
est divisible par deux. Comme
 est un nombre pair,
est un nombre pair,  l'est aussi.
l'est aussi.Or si
 est divisible par deux, alors
est divisible par deux, alors  tel que
tel que  .
.Nous pouvons alors écrire
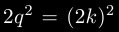 et donc
et donc  . Maintenant nous constatons que
. Maintenant nous constatons que  est divisible par deux, donc a fortiori
est divisible par deux, donc a fortiori  aussi.
aussi.Nous avons obtenu
 et
et  divisible par deux, or nous avons supposé
divisible par deux, or nous avons supposé  et
et  premiers entre eux, donc il y a bien contraction de l'hypothèse.
premiers entre eux, donc il y a bien contraction de l'hypothèse.Alors
 est un nombre irrationnel. (CQFD)
est un nombre irrationnel. (CQFD)Et maintenant la preuve.
Démontrons maintenant qu'il existe deux nombres irrationnels
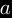 et
et  tels que
tels que 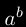 soit rationnel.
soit rationnel.Notre preuve s'appuie sur la loi du tiers exclu qui en formulation
simple suppose qu'une proposition est soit vraie ou fausse.
Posons
 et
et  .
.Nous avons
 et deux cas se présentent:
et deux cas se présentent:1) Soit
 est un nombre rationnel, dans quel cas nous avons trouvé un rationnel validant la proposition.
est un nombre rationnel, dans quel cas nous avons trouvé un rationnel validant la proposition.2) Soit
 est irrationnel.
est irrationnel.Dans quel cas nous posons
 et
et  . En effet, nous avons bien établi l'irrationalité de
. En effet, nous avons bien établi l'irrationalité de  et nous avons
et nous avons  .
.En simplifiant, nous obtenons
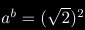 , soit
, soit  , un rationnel.
, un rationnel.Dans les deux cas, nous obtenons un nombre rationnel.
Mot de la fin
Cette preuve est d'autant plus intéressante qu'elle fait appel au principe du tiers exclu qui est un raisonnement logique rejetté dans une démonstration constructive.
!Erreur!
Je remercie le commentaire anonyme pour avoir signalé l'erreur dans cette preuve. Voir les commentaires.


2 Comments:
koi???
mai comment tu peu simplifier kom sa (a exposant b)?? jvoi pa d'ou sort cette egalite...
Bien vu et merci ;o)
Il y a bien erreur d'écriture ici.
Donc,
si on posait a commme rac(2) exp rac(2) et b = rac(2), alors on aurait:
a^b = (rac(2)^rac(2))^rac(2) = rac(2)^2 = 2
Enregistrer un commentaire
<< Home